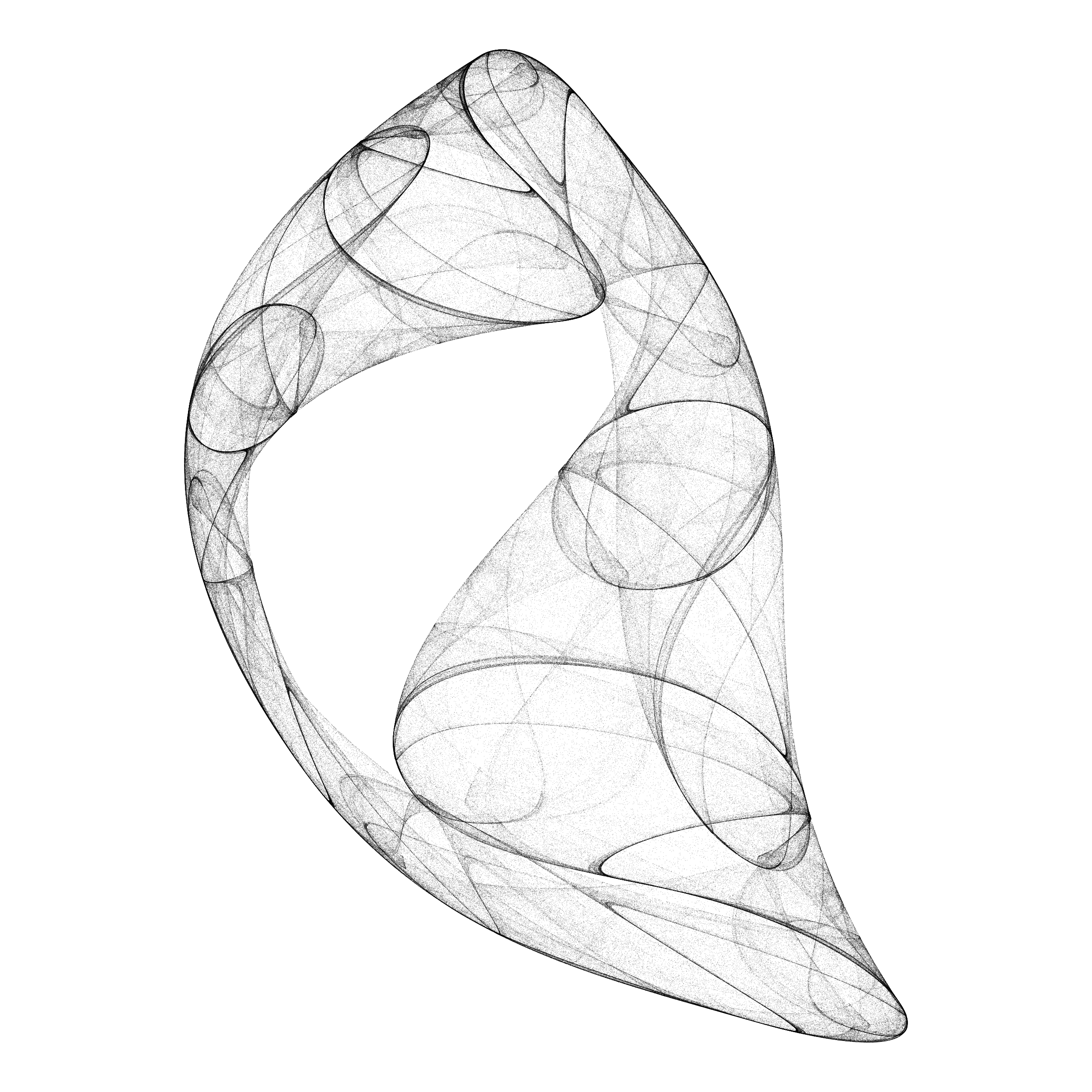
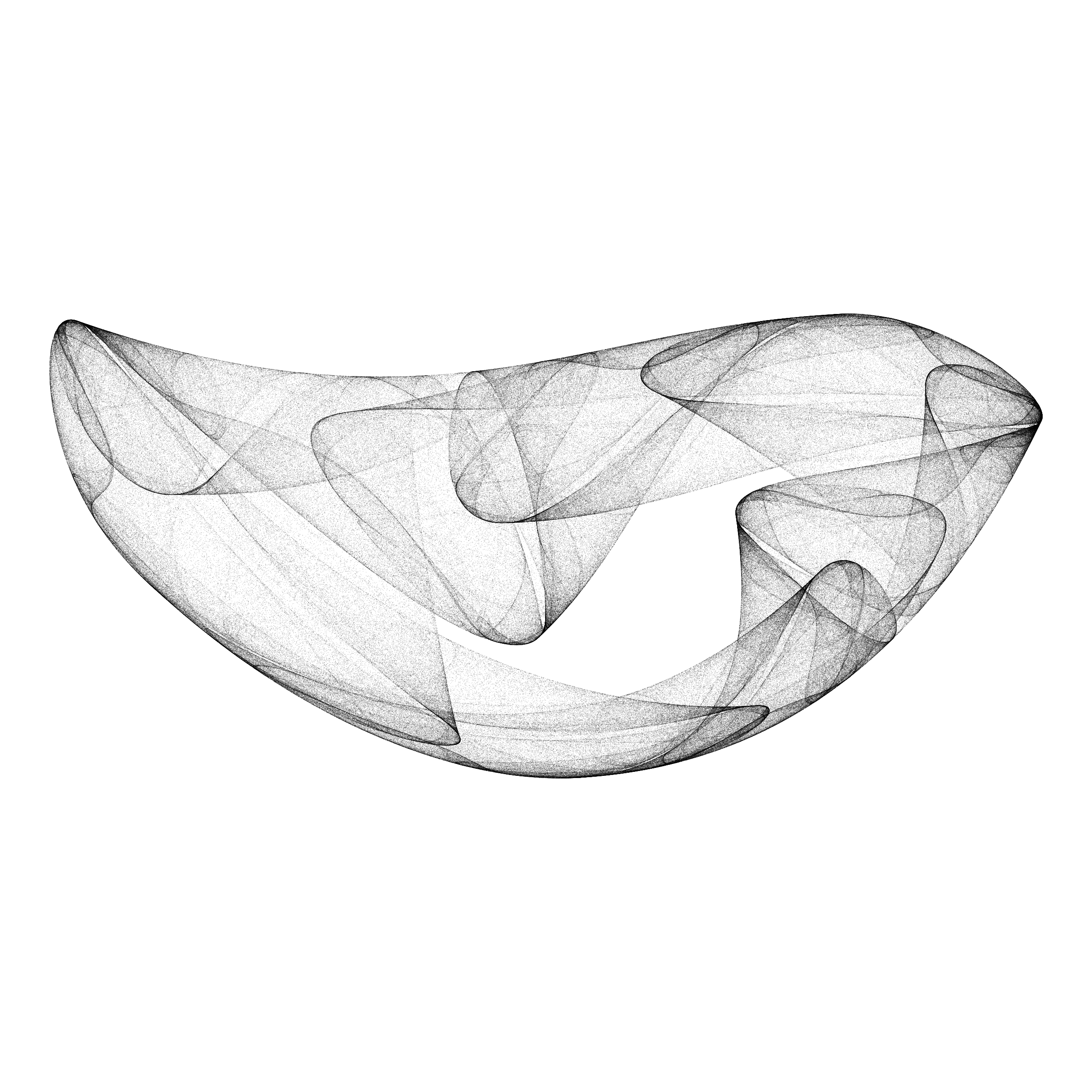
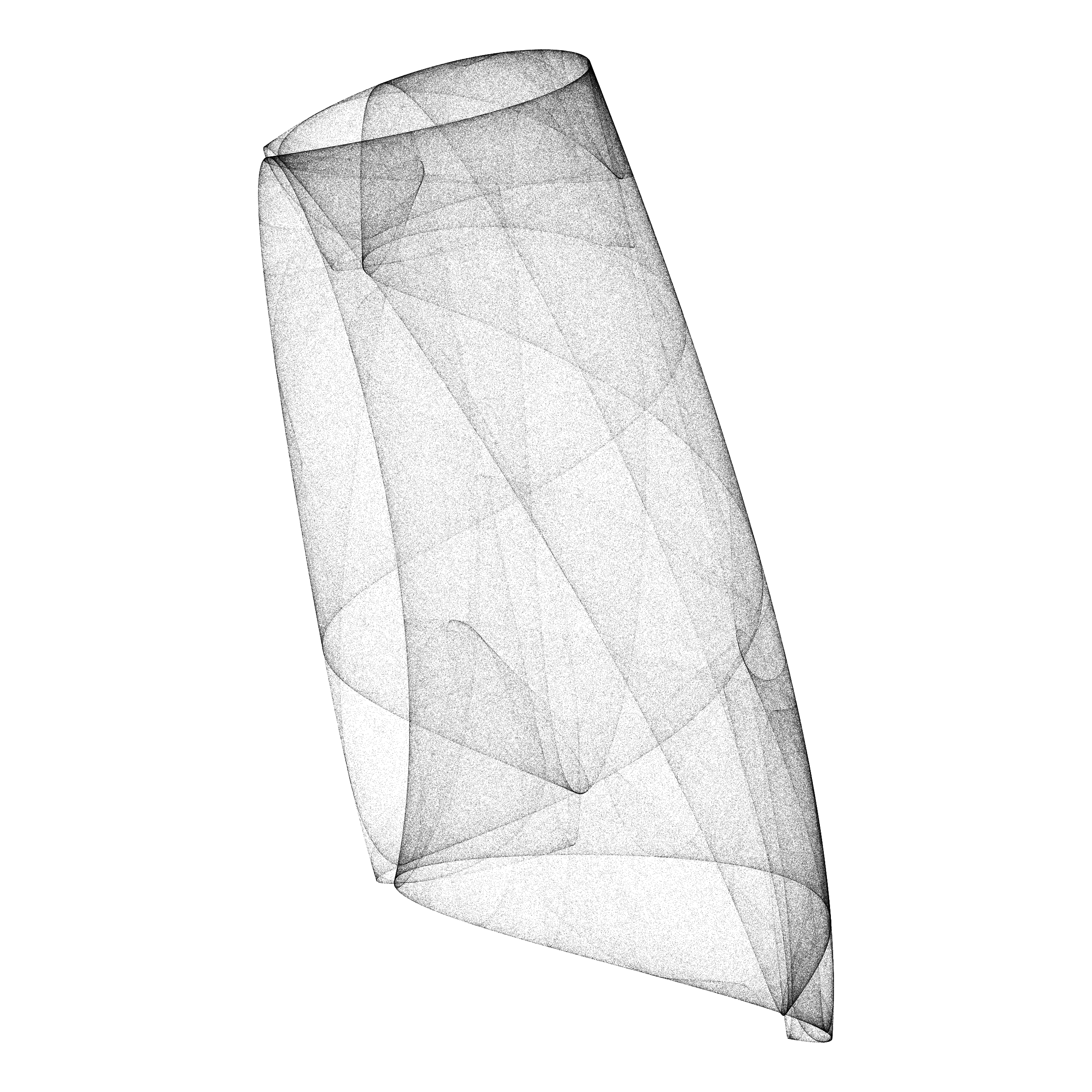
Aesthetic point sets generated by discrete dynamical systems.
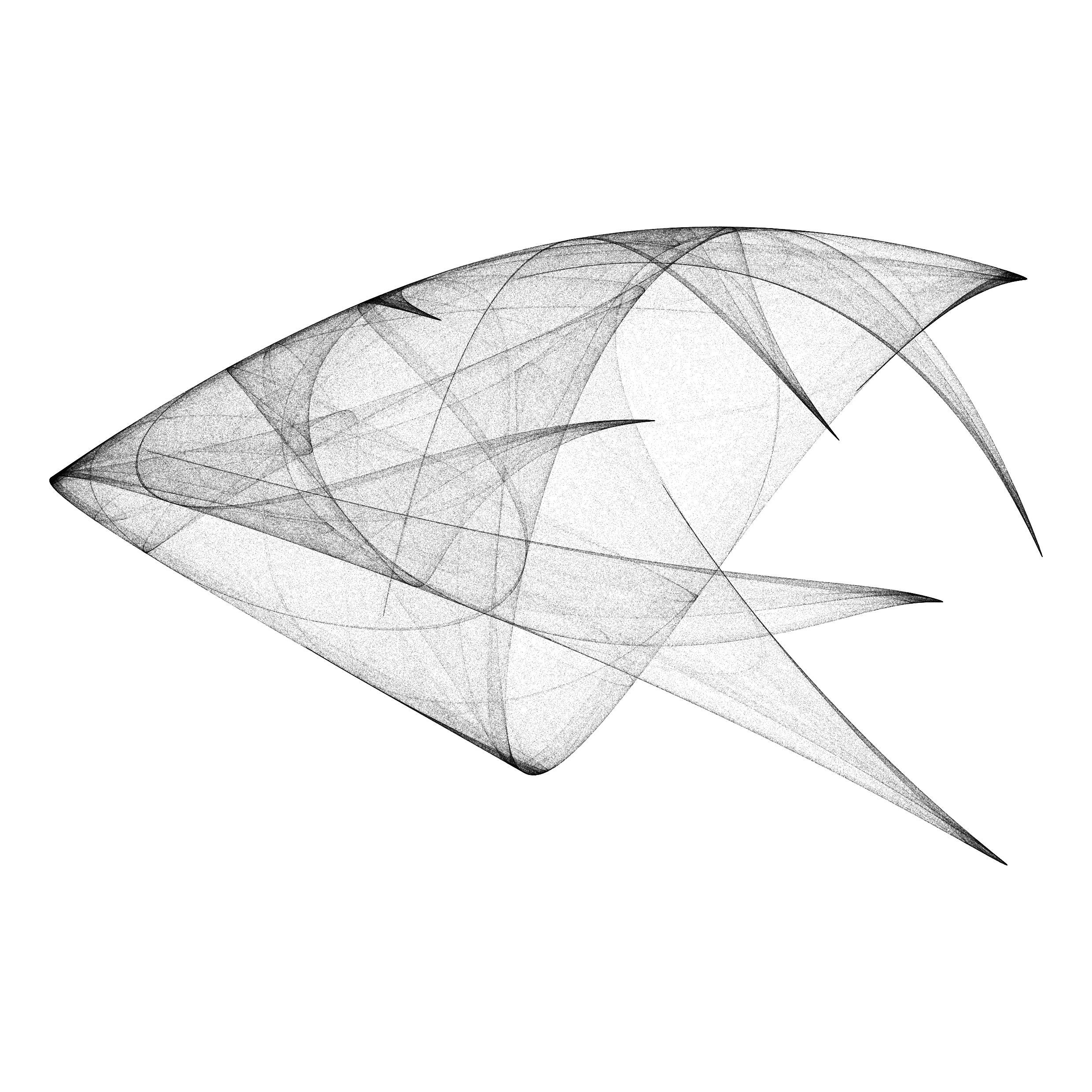
This work explores the capacity of discrete dynamical systems to generate a large diversity of point sets. It is based on this paper from J.C Sprott in 1993, recently reproduced by Paul Bourke. Henrik Lindberg also published an R implementation of the quadratic map functions used here.
The algorithm is based on a system of difference equations, with 12 parameters. The first step is to sample the parameter space by using a discrete scale of 26 values for each parameter so that each sample can be assigned a “name” with 12 letters. A second step discards failed solutions (convergence to a point, divergence) and filters the aesthetic ones, based on a set of criteria (Lyapunov exponent, summary of point density distribution, correlation). Overall, very few solutions are selected (~ 0.1 %).
While this method is a very good generator for diverse 2D shapes, it is not compatible with pen-plotting because of the difficulty to create paths from those point sets - the points are not ordered by the iterations of the difference equation, and jumps from one position to another. One solution is to define the relative neighbourhood graph on a subsample of the simulated set of points.